约束满足问题使用分解成因子的表示法(a factored representation)来描述状态
一元约束:只限制单个变量的取值
二元约束:与两个变量相关的取值
全局约束:变量数任意的约束
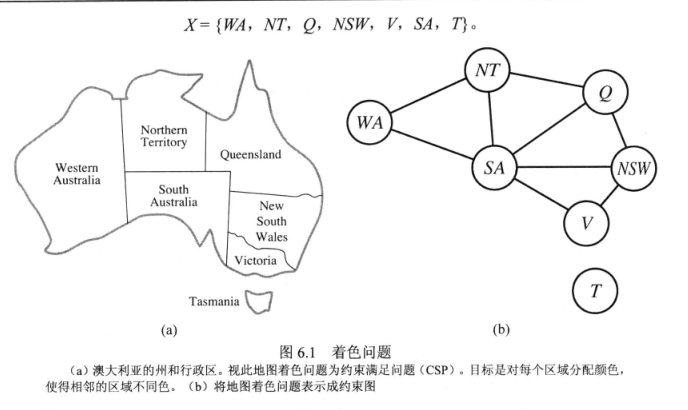
例子:
约束传播——CSP中的推理
什么是约束传播:约束传播是CSP算法中的一种用约束来减小一个变量合法取值范围的特殊推理
局部相容性:将变量看作图中的节点,约束看作图中的弧,相容性指不相容的节点取值被删除
节点相容:单个变量(CSP网络中节点)值域中所有的取值满足它的一元约束
弧相容:称变量x_i相对x_j是弧相容的若对于x_i的所有取值,x_j都存在取值使得弧(x_i,x_j)是相容的
若每个变量相对其他变量都是弧相容的,则称该网络是弧相容的

AC-3算法也适用于有向图
路径相容:两个变量的集合{x_i,x_j}对于变量x_m是相容的若对{x_i,x_j}的每一个赋值,x_m都有合适的取值同时使得{x_i,x_m},{x_j,x_m}是相容的
k-相容:对于任意k-1个变量任意相容的赋值,第k个变量都存在与前k-1个变量相容的赋值,则称这k个变量是k-相容的;称一个CSP图是k-相容的若任意k个节点都是相容的,是强k-相容的若k,k-1,……,1相容的
全局约束
资源约束
边界相容
部分赋值的回溯搜索算法
CSP回溯搜索伪代码:

简单回溯算法中三个可以具体化的函数:
1)下一步给哪个变量赋值(SELECT-UNASSIGNED-VARIABLE),按照什么顺序尝试它的值(ORDER-DOMAIN-VALUES)?
2)每步搜索应该做什么样的推理(INFERENCE)?
3)当搜索到达的某赋值违反约束时,搜索本身能避免重复这样的失败吗?
1)对于选择变量,应当选择“最有可能导致失败”的变量,有助于剪枝,常用启发式有最少剩余值(MRV)启发式,度启发式。
最少剩余值启发式选择值域最小(即受约束限制最多)的变量,利于剪枝;度启发式选择到其余未赋值变量连接最多的(有向)边最多的变量,利于打破僵局;
对于选择一个变量的取值顺序,应当选择“最有可能导致成功”的赋值,常用的启发式有最少约束值启发式。
最少约束值启发式优先选择给其指向的节点更大赋值空间的赋值,这有利于找到解。
变量选择采用失败优先策略而赋值选择采用成功优先策略,目的是选择具有较少赋值空间的变量可以通过早期剪枝而减少搜索树的节点数,选择导致更大赋值空间的赋值有利于找到解。但要注意的是如果目标是枚举所有解而不是找到一个解,对于赋值的选择策略将毫无意义。
2)对于推理,书中介绍了两种推理方法,一种是简单的向前检验,一种是维护弧相容(MAC)算法。
向前检验对当前赋值变量进行弧相容检验,每个通过约束与当前赋值变量相关的未赋值变量,都要将其值域中与当前赋值变量不相容的值。向前检验的无法检测出所有不相容,例如两个相关的未赋值变量有可能存在的不相容是检验不出来的。
MAC弧相容维护算法对通过以当前赋值节点相邻的弧为起点的AC-3算法进行约束传播,一旦发现某变量的值域为空,则调用失败并回溯。
向前检验第一步与MAC算法相同,但是向前检验不传播约束,MAC算法传播约束。
3)简单的搜索不能避免重复陷入同一个违反约束的变量赋值组合。此处介绍了两种方法避免重复陷入同一个违反约束的变量赋值组合。冲突集:使得当前变量值域为空的一组变量的赋值。
回跳法,通过简单地定义冲突集来确定回跳变量。缺点是只能进行一层回跳。若使用的是向前检验算法或者更强的MAC弧相容维护算法,则冲突集不需要额外的工作就能得到,且根本不会陷入这种情况。
冲突指导的回跳,每次回跳都拓展冲突集的回跳,可以多层回跳。
约束学习:从冲突集中找出导致问题冲突的最小变量赋值集合(这些集合称为无用)。
向前检验和回跳都可以有效地使用无用,约束学习是现代CSP求解器有效求解复杂问题的重要技术之一。
回溯算法中
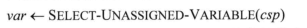
此处是简单的静态排序,可以使用启发式来剪枝提高搜索效率
如最少剩余值(MRV)启发式挑选“最受约束”、“最可能很快导致失败”的变量,或者度启发式来挑选约束最多的未赋值变量试图降低未来的分支因子
CSP局部搜索
最少冲突启发式伪代码:

即从当前解中随机选取一个存在冲突的变量,为这个变量重新赋以与其他变量冲突最少的值
完整赋值的局部搜索
完整赋值的初始状态是一个随机的布局,会违反某些约束,局部搜索的目的就是消除这些矛盾。
两种策略:最少重复启发式,约束加权
最少冲突启发式用于选择变量的赋值,为变量选择导致最小冲突的赋值
加权约束用于选择变量——将每个约束赋以权值,并加权称为评价函数。
4.1中的局部搜索算法都可以应用在CSP搜索中
问题的结构
假设直接求解n个变量d种赋值的CSP问题的时间复杂度是 ,若分解为 个子问题,则时间复杂度将为
对于树状结构的CSP问题,有线性时间复杂度的求解算法

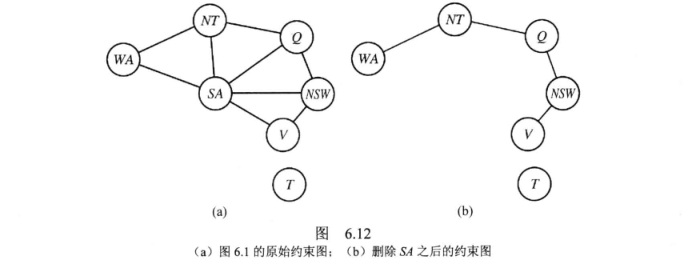
考虑将一般的CSP问题分解,这里介绍了两种方法:基于删除节点的方法,基于合并节点的方法
1)环割集

时间复杂度
找出最小环割集的是NP难问题,但可用割集调整近似算法来求解
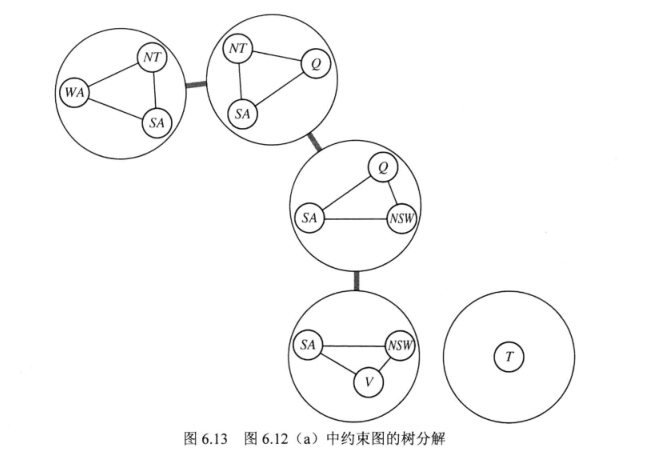
2)树分解
树分解必须满足三个条件: