什么是基于知识agent
知识库?知识表示语言的语句形式?推理?
语法、语义?
语句之间的涵盖关系?
可靠的推理算法只生成被蕴含的语句
完备算法生成所有被蕴含的语句、
命题逻辑:命题词和逻辑连接词
用于命题逻辑的有效模型检验推理算法包括回溯和局部搜索方法,可快速求解大规模问题
推理规则:寻找证明的可靠推理模式
消解规则:用在表示为合取范式的知识库上的完备推理算法。
前向连接和反向连接都是用在Horn子句表示的知识库上的自然推理算法
局部搜索算法如WALKSAT可以用于问题求解,可靠但不完备
逻辑状态评估需要维护与观察历史一致的描述可能状态集的逻辑语句
每一更新步骤要求使用环境的转移模型,转移模型可以从后继状态的公理构建
逻辑的Agent巨册可以公国SAT求解:找出模型规范到达目标啊的未来可能的行动序列。
这种方法只适用于完全可观察或无传感信息的环境
命题逻辑无法扩展到无限环境,因为它无法准确地处理时间、空间及对象关系的模式
基于知识的Agent的总体设计
新的简单环境Wumpus世界
逻辑的一般原理
命题逻辑,逻辑的基本概念
命题逻辑定理证明
有效的命题逻辑模型检验
基于命题逻辑的Agent
知识库KB:核心部件,是一个语句集合,用知识表示语言表达,公理—:直接给定而不是推导得到的语句
TELL操作和ASK操作都可能涉及推理

知识库的分析独立于实现层,不关心知识是以链接列表还是响速地图的形式实现,或者是处理存储在寄存器中的符号串还是在神经网络中传递有噪音的信号来进行的。
陈述性方法:将知识以语句形式通过TELL告知知识库
过程性方法:将行为直接写为程序代码
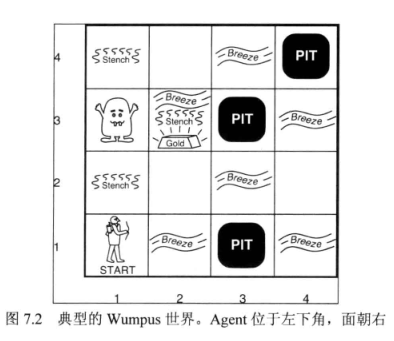
Wumpus世界给出了一个简单的基于知识的Agent的例子,用PEAS描述
性能度量:带着金子爬出洞口+1000,挂掉-1000,采取一个行动-1,射箭-10,死亡或者出洞口游戏结束
环境:4X4房间网格,可能有无底洞或者Wumpus
执行器:上下左右均可移动(如果房间存在),撞墙无法前进,拾取,射箭,爬出(只可从起点(1,1)爬出)
传感器:在与无底洞相邻的房间感知到Breeze;在与Wumpus相邻的房间感知到stench;在金块放置的房间感知到Gold;撞墙时能感到撞击;Wumpus被杀死时能感知到嚎叫
语句:知识库的构成
语义:语句的含义,语义定义了每个语句在可能世界的真值
语法:语句遵循表示语言的语法
可能世界:Agent潜在的真实环境
模型:可能世界的数学抽象。例如对于x+y=4,可能模型就是x和y所有可能的赋值;这样的赋值决定了任何含有变量的x和y的算数语句的真值。
如果语句 在模型 中为真,则称 满足 ,也称 是 的一个模型;用 表示所有的模型。
蕴含:某语句逻辑上跟随另一个语句,数学表示为 ,意为语句 蕴含语句 ,其等价定义为 ,即 是比 更强的断言,排除了更多的可能世界
逻辑推理:结合模型用蕴含推导出结论
模型检验:通过枚举所有可能模型(可能世界的数学抽象)来检验知识库KB为真的情况下语句α是否为真
枚举所有的模型,并验证语句在所有的模型中为真。
可靠/真值保持:只导出蕴含语句的推理算法被称为可靠的或者真值保持的
模型检验在可行的情况下是可靠的?
可行:如果模型空间是有限的,那么模型检验是有效的,例如在大小固定的Wumpus世界里。另一方面,对于算数问题模型空间是无限的,即使限制在整数范畴,对于句子x+y=4仍然存在无数对x和y的值
完备性:推理算法可以生成任一蕴含句。
原子语句:原子语句由单个命题词组成,每个命题词代表一个或真或假的命题,用大写字母表示命题词
复合句:由简单语句用括号或逻辑连接词构造而成,常用的逻辑连接词有:与 ,或 ,非 ,蕴含 ,当且仅当(双向蕴含)
语义定义了用于判定特定模型中语句真值的规则
命题逻辑固定了每个命题词的真值,不能既真又假
命题逻辑通过递归来计算任一语句的真值
复合句的五条规则:

连词的运算规则可以用真值表总结:
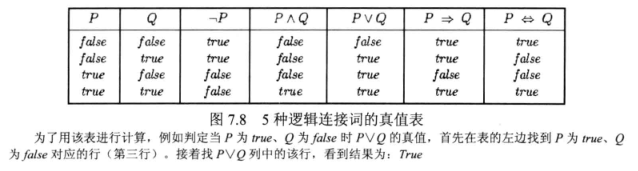
提问:什么是蕴含?
语句“5是奇数蕴含东京是日本首都”是命题逻辑的真语句,符合真值表,同样的“东京是日本首都蕴含5是奇数”也是命题逻辑的真语句,符合真值表。
那么“5是奇数当且仅当东京是日本首都”这样的虽然是真语句,但是有意义吗?前后两个原子语句的真假似乎是无关的。
例子:

除了可以使用模型检验来判断蕴含,还可以使用定理证明来判断蕴含
逻辑等价:如果两个语句在同样的模型集合中为真,则它们是逻辑等价的,写作 ;等价的定义是两个语句等价当且仅当它们相互蕴含
标准逻辑等价
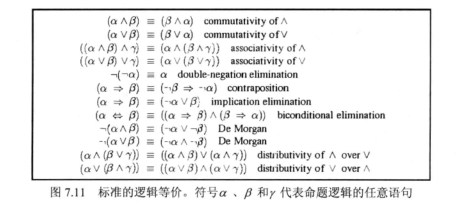
有效:一个语句是有效,如果它在所有的模型中都为真,有效语句也称为重言式——它们必定为真
演绎定义:对于任意语句 , 当且仅当语句 是有效的
提问: 与 是什么关系? 与 是什么关系?
连接前后两个语句,在不同模型中有不同的取值,可为真,可为假
连接前后两个语句,表示在所有可能的模型中,关系都成立
可满足性:一个语句在某些模型中为真,那么这个语句是可满足的。验证一个语句是否是可满足的可以通过枚举所有的模型来进行。
命题逻辑语句的可满足性判定——SAT问题——是第一个被证明为NP完全的问题,例如所有约束满足问题中询问在某个赋值下的约束是否为可满足的。
有效性和可满足性的关系: 是有效的当且仅当 是不可满足的
如此可以得到一个有用的结论: 是有效的当且仅当语句 是不可满足的,亦即当且仅当语句 是有效的(这里使用的方法被称为反证法或矛盾法)
单调性:逻辑蕴含语句集会随着添加到知识库的信息增长而增长
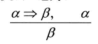
亦即给定任何形式为 和 的语句,就可以导出语句
例如从 和 ,可以推导出
提问:按照真值表如何推出如上的例子?
当 为false, 为true时, 也可以为false

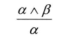
即从合取式可以推导出任何合取子句
提问:如何推出?
例子:


可以用搜索证明替换模型枚举方法,只需要如下定义证明问题:
1)初始状态:初始知识库
2)行动:行动集合由应用于语句的所有推理规则组成,要匹配推理规则的上半部分
3)结果:行动的结果是将推理规则的下半部分的语句实例加入知识库
4)目标:目标是指包含要证明的语句的状态
当归结于任何一个完备的搜索算法相结合时,可以得到完备的推理算法


以句子的合取式表达的语句被称为合取范式或者CNF
合取范式的步骤如下

归结算法的步骤:
为了证明 ,需要证明语句 是不可满足的
1)将 转换为CNF
2)对结果子句运用归结规则,对含有互补文字的子句进行归结产生新子句,如果该子句尚未出现过,则将之加入子句集中
3)重复1)2)直到以下两种情况之一发生:没有可以添加的新子句(KB不蕴含α),两个句子归结出空子句(KB蕴含α)