邻接表:第一下标代表顶点编号第二下标范围可变的二维数组存储图
邻接矩阵:二维数组(矩阵)存储图
邻接多重表:
每条边用一个节点表示

每个顶点也用一个节点表示

无向图
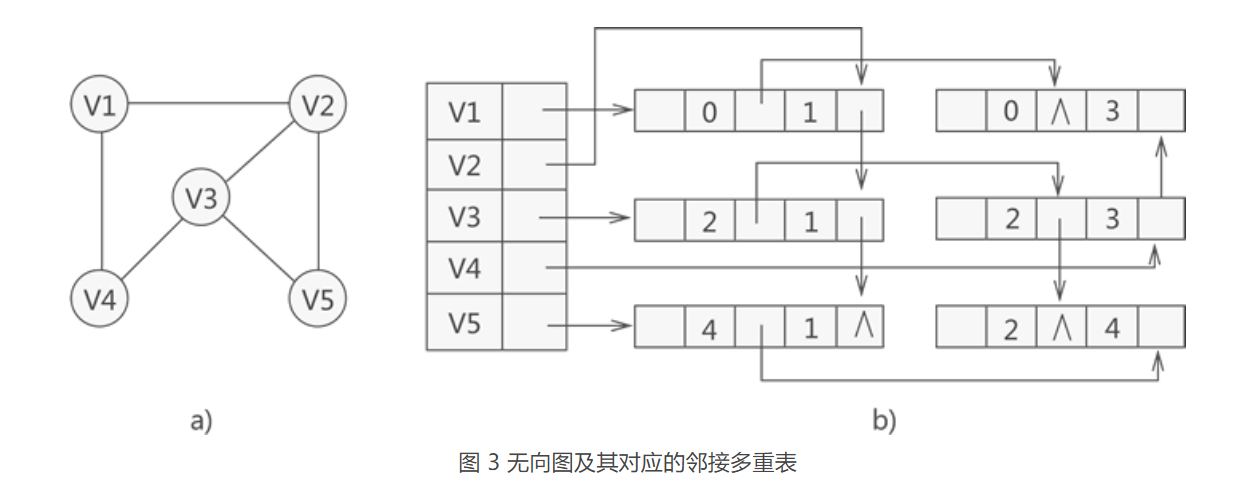
与邻接表不同的是:同一条边在邻接表中用两个节点表示,而在邻接多重表中只用一个节点表示
邻接多重表只用来存储无向图
十字链表
对于有向弧<va,vb>,va称为弧尾,vb称为弧头
十字链表的弧和顶点用以下两种结点表示

hlink指向下一个以headvex为弧头的弧,tlink指向下一个以tailvex为弧尾的弧
firstin指向第一个以该顶点为弧头的弧,firstout指向第一个以该顶点为弧尾的弧
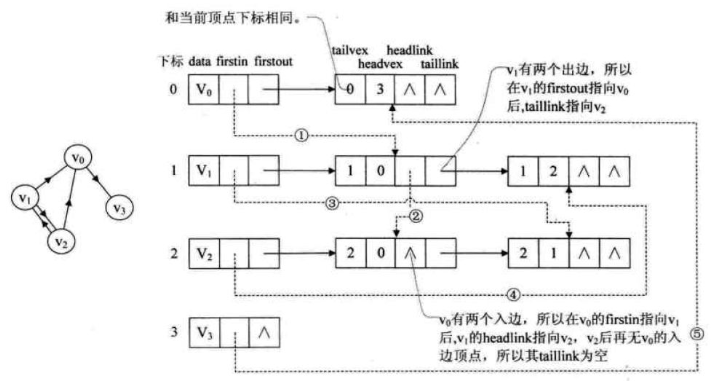
十字链表只用来存储有向图
一些基本概念
连通分量
从图中某一顶点出发进行图遍历,能访问到该顶点所在的最大连通子图的所有顶点,这些顶点构成一个连通分量
重连通分量
在一个无向连通图中称一个节点为关节点,当且仅当删去这个节点以及所有依附于其的边之后,这个连通图被分割成至少两个连通分量
一个没有关节点的连通图(连通分量)称为重连通图(重连通分量)
有向图的强连通片
有向图中,两个节点能够相互到达,则称这两个节点为强连通的。一个有向图是强连通的若任意两个节点之间都是强连通给的。有向图的强连通片是其极大强连通子图。
如果把每个强联通篇收缩成一个点,强连通片收缩成一个点,强连通片之间收缩成一条有向边,则得到G的收缩图。
k-点连通,k-边连通
对于连通的无向图,如果去掉任意k-1个点,图仍然连通,则这个图是k-点连通的;如果去掉任意k-1条边,图仍然连通,则这个图是k-边连通的
割点与桥
称某个节点为无向连通图的个点,如果去掉该节点依赖它的边之后之后图不再连通;称某条边为桥,如果去掉这条边之后该图不再连通
简单路径和简单回路
简单路径:所有顶点不重复出现
简单回路:除了第一个顶点和最后一个顶点之外其余顶点都不会重复出现
AOV网络(顶点表示活动的网络)与拓扑有序
AOV网络不能存在有向环
拓扑有序,节点保持前驱后继关系保持相对不变
通过深度优先遍历退回时返回节点,可以得出拓扑逆序序列
AOE网络(边表示活动的网络)与关键路径
完成整个工程所需的时间取决于从源点到汇点的最长路径的长度,即在这条路径上所有的活动持续的时间之和。
这条路径长度最长的路径就叫做关键路径。
如何求关键路径?
1)顺序求解每个顶点(作为活动起点的事件)的最早发生时间ve
2)逆序求解每每个顶点(即事件)的最晚发生时间vl
3)根据各个顶点(事件)的ve求各条边(活动)的最早开始时间e
4)根据各个顶点(时间)的vl求各条边(活动)的最晚开始时间l
5)所有最晚开始时间等于最早开始时间的活动都是关键活动,它们构成关键路径