无向图,有向图
有向图D中顶点 的入度记为 ,出度记为
阶数:顶点的个数,具有n个顶点的图称作n阶图
零图:没有边的图
空图:顶点集为空的图
关联:描述顶点与边的关系的概念,称边e与顶点v关联,若v是e的一个短点。若边e的顶点只有一端是v,则v与e的关联次数为1,特别地若e的两个端点都是v,则v与e的关联次数为2
相邻:称两个顶点相邻若它们为某条边的两个端点,在无向图中称两条边相邻若他们共享同一个顶点为端点,在有向图中称两条边相邻,若一条边的终点是另一条边的起点
度数:顶点的度数指以某一顶点为端点的边的条数,特别地在有向图中,顶点的出度为以某一顶点为起点的边的条数,顶点的入度为以某一顶点为终点的边的条数
悬挂顶点:度数为1的顶点
悬挂边:与悬挂顶点关联的边
最大度:某图中顶点的最大度数,记为
最小度:某图中顶点的最小度数,记为
最大出度、最小出度、最大入度、最小入度:定义类似
平行边:在无向图中,关联一对顶点的边的条数若多于一条,则称这些边为平行边。在无向图中,关联一对顶点的边若多于一条,且它们的起点与终点相同,则称这些边为有向平行边,简称平行边。
环:两端点重合的边
重数:边的重数为与之两端端点相同(或起点与终点相同)的平行边的条数
多重图:含有平行边的图称为多重图
简单图:不含平行边也不含环的图称为简单图
完全图:记作
k-正则图:各个顶点度数均等于k的无向简单图
n阶圈图:

n阶轮图:

n方体图:

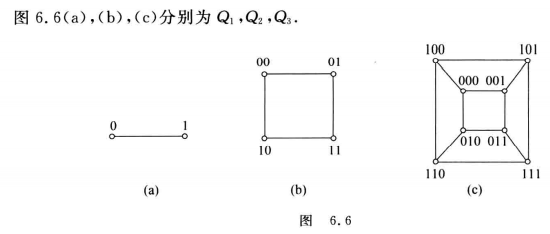
真子图:顶点集和边集都是原图的真子集
生成子图:顶点集等于原图的顶点集
导出子图:非空顶点集 为原图的子集,边集由两个端点均在顶点集中的边的全体组成的图,记作 ;非空边集 为原图的子集,顶点集由所有与边集中的边相关联的顶点的全体组成的图,记作
补图:以所有能使简单无向图 成为完全图 的添加边组成的集合为边集的图称为 相对于 的补图,记作
图的同构:
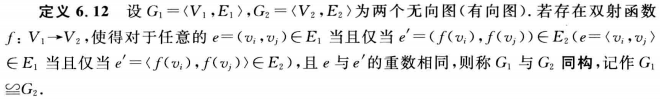
通路与回路:若图 中的顶点和边的交替序列 满足 分别是 的起点和终点,则称序列 为从 到 的通路。特别地,当 时,称通路为回路。
简单通路和简单回路:若通路中所有的边都互异,则称通路为简单通路;特别地,称起点等于终点的简单通路为简单回路。
初级通路和初级回路:通路中所有的顶点都互异,则称通路为初级通路或初级路径;特别地,称起点等于终点的初级通路为初级回路或圈。(注意:圈不是环)
复杂通路和复杂回路:若通路中有重复边出现,则称通路为复杂通路;特别地,称起点与终点相同的复杂通路为复杂回路。
连通图:
在无向图G中,若两个顶点之间存在通路,则称这两个顶点是连通的。若无向图G是平凡图或者G中任意二顶点都是连通的,则称G是连通图,否则称G是非连通图。
在有向图D中,如果略去各边的方向所得的无向图是连通图,则称D是弱连通图或者连通图;弱D中任意两个顶点至少一个可达另一个,则称D是单向连通图;若D中的任意两个顶点都是相互可达的,则称D是强连通图。
可达:在有向图中,对于顶点u和v,若存在从u到v的通路,则称u到v是可达的;若u到v与v到u都是可达的,则称u和v相互可达
短程线:称两个顶点之间长度最短的通路为两个顶点之间的短程线,短程线的长度称为两点之间的距离,在无向图中记作 ,在有向图中记作
割集:对于无向图 ,若顶点集 ,则称顶点集 是点割集。若边集 ,则称边集 是边割集。点割集和边割集都可简称为割集,若点割集只有一个点,则称该顶点为割点,若边割集只有一条边,则称该边为割边或者桥。
连通分支:由连通关系划分的顶点的等价类的导出子图,连通分支数目记作
连通度:
点连通度——元素个数最小的点割集的元素个数,记作
边连通度——元素个数最小的边割集的元素个数,记作
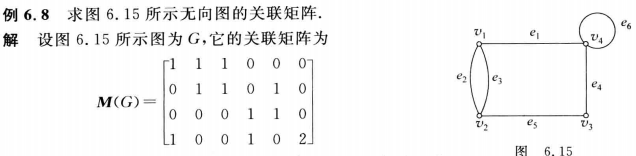
无向图的关联矩阵:
对于无向图 ,其关联矩阵记作 ,其元素 表示顶点 与边 的关联次数
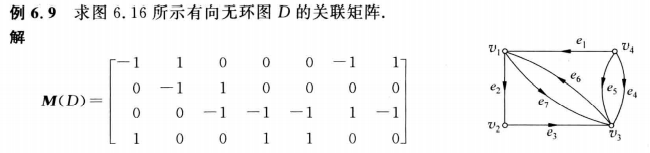
有向无环图的关联矩阵:
对于有向无环图 ,其关联矩阵记作 ,其元素 若顶点 是边 的起点, 若顶点 是边 的终点, 若顶点 与边 不关联
有向图的邻接矩阵:
对于有向图 ,其邻接矩阵记作 ,其元素 表示从顶点 到顶点 的边的条数
有向图的可达矩阵:
对于有向图 ,其可达矩阵记作 ,其元素 若 可达 ,否则
二部图:
对于无向图 ,若其顶点集能分为两个不相交子集 ,且任意边的两个端点都分别属于 ,则称 为二部图
欧拉图:
对于连通图 ,若 中存在欧拉回路,则称 为欧拉图
欧拉通路:经过且仅经过一次图中每条边的通路,简言之就是经过所有边的简单通路
欧拉回路:经过且仅经过一次图中每条边的回路,简言之就是经过所有边的简单回路
哈密顿图:
对于连通图 ,若 中存在哈密顿回路,则称 为哈密顿图
哈密顿通路:经过且仅经过一次图中每个顶点的通路,简言之就是经过所有顶点的初级通路
哈密顿回路:经过且进经过一次图中每个顶点的回路,简言之就是经过所有顶点的初级回路
平面图:
若图能以除了顶点之外没有边的交叉出现的方式画在平面上,则称图为平面图,此种方式称为平面嵌入或平面表示
握手定理:任意图中,所有顶点的度数之和等于边数之和的两倍
握手定理推论:任意图中,度数为奇数的顶点个数为偶数
无向简单图最大度:无向简单图的最大度满足
有向图度数定理:有向图中,所有顶点的出度之和等于所有顶点的入度之和,为边数之和
完全图边数:在无向完全图中,边数 ,在有向完全图中,边数
初级通路存在性及其长度定理:在一个n阶图中,若两个顶点之间存在通路,则这两个顶点之间必然存在长度不超过n-1的初级通路
初级回路存在性及其长度定理:在一个n阶图中,若某个顶点存在到自身的简单回路,则这个顶点存在到自身的长度不超过n的初级回路
点割集和边割集的连通分支数目: 是连通图, 是边割集,则 ; 是点割集,则
连通度定理:对于任意无向图 ,有
二部图判别定理:无向图是二部图当且仅当它没有长度为奇数的回路
无向欧拉图的判别定理:无向图为欧拉图当且仅当图连通且无奇度顶点;无向图有欧拉回路当且仅当图连通且有两个奇度顶点
有向欧拉图的判别定理:有向图为欧拉图当且仅当图连通且每个顶点的入度等于出度;有向图有欧拉通路但无欧拉回路当且仅当图连通且一个顶点入度比出度大于,另一个顶点出度比入度大于1,其余顶点入度均等于出度
哈密顿图的一个必要条件:无向图为哈密顿图,则对于顶点集的任意子集 ,均有
哈密顿图的一个充分条件:大于二阶的无向见到那图,若图中任意两个不相邻的顶点 ,均有

注意:
(1)阶数+边数+度数列不能唯一确定图
(2)根据阶数和边数以及握手定理的推论可以得出一系列可行的度数列
无向图的关联矩阵
有向无环图的关联矩阵
有向图的邻接矩阵


注意:简单图是没有平行边也没有环的图
无向图中,平行边指的是两条端点相同的边;有向图中,平行边指的是两条起点与终点分别相同的边;
环指的是起点和终点重合的边;圈指的是初级回路(路径上的顶点不重复出现)

注意:可以使用归谬法

注意:由6.13的结论知一个图的补图在同构的意义下是唯一的;注意可以带圈,带圈的可能是简单图,只要不是环

注意:生成子图——顶点集与原图顶点集一样的子图
注意:鸽笼原理——n个鸽子飞进m个笼子里,至少有一个鸽笼至少飞入了 个鸽子
注意:存在有圈的子图,不要漏掉

注意:每个在原图中度为奇度的顶点,其在补图中的度一定也为奇度,因为在完全图中每个顶点的度都为偶
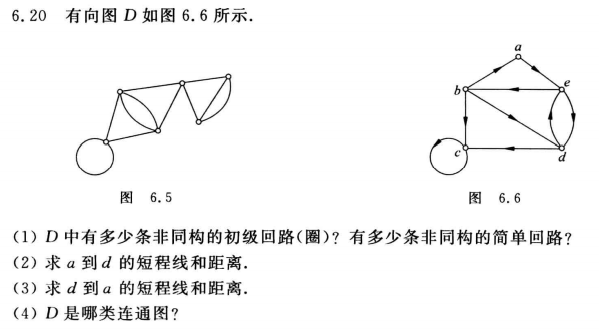
注意:不要漏了,还有单连通图这种类型