二叉树(完全二叉树、满二叉树)、线索二叉树、Huffman树、
堆、二叉搜索树、AVL树、
多叉树、森林、
并查集、
B树、B+树
树的深度:距离根节点最远的叶节点的层次
树的高度:叶节点的高度为1,非叶节点的高度为其子节点高度的最大值加1
节点的度:节点所拥有的子节点的个数
树的度:书中节点的度的最大值
二叉树只有至多只有两个子节点,分别为左孩子和右孩子
性质:
1)二叉树在第i层最多有 个节点
2)深度为k的二叉树至少有k个节点,至多有 个节点
3)二叉树的节点总数有两种表示:
4)
深度为k的具有 个节点的二叉树
具有n个节点,深度为k的且与深度为k的满二叉树的1-n号节点一一对应的二叉树
性质:
1)具有n个节点的完全二叉树深度为
2)节点编号为1-n的完全二叉树的第i个节点所在的层次为
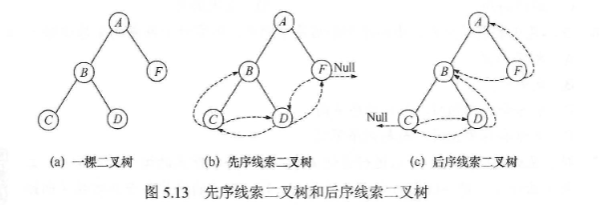
按照一定的遍历顺序(如先中后序遍历)为每个节点额外建立前驱后继关系的二叉树称为线索二叉树
中序线索二叉树的构造
若节点无左子树,则前驱指针指向中序序列中的前一个节点;若节点无右子树,则后继节点指向中序序列的后一个节点
前序和后序线索二叉树
定义扩充而战术为叶节点带有权值的二叉树,带权的叶节点叫做外节点,不带权的非叶节点叫做内节点。
扩充二叉树带权路径长度定义为 ,其中 为外节点的权值, ,为外节点的路径长度
带权路径长度最小的二叉树,即权值越大的外节点里根节点越近的扩充二叉树,被成为Huffman树
1)根据给定的n个权值 ,构造具有n棵扩充二叉树的森林 ,各个树都是一个只带权值的根节点
2)重复以下步骤,直到森林中只剩下一棵树:
从森林中选取两颗根节点的权值最小的两颗扩充二叉树,作为左右子树构造一棵新的二叉树,新的二叉树的根节点的权值为其左右子树的根节点上的权值之和
前缀编码:变长编码集中必须保证任意一字符编码都不是其他字符的前缀
对于k路最佳归并树,可以将二叉树Huffman树的构造方法推广
假设有 个叶节点,且 ,则当 时可以直接推广;
当 不能被 整除时,添加 个权值为0的空段作为外节点,与最初的森林一起归并
按照完全二叉树的顺序存储方式存储,并且满足子节点的值不大于(不小于)父母节点的值的树叫做大顶堆(小顶堆)
二叉搜索树是具有以下性质的二叉树:
1)每个节点上都有一个作为唯一搜索依据的值,所有节点的值互不相同
2)左子树上的节点的值都小于根节点的值
3)右子树上的结点的值都大于根节点的值
4)左子树和右子树都是二叉搜索树
二叉搜索树的删除:
搜索到待删除的节点后,删除该节点,若该节点是叶子节点,直接删除;
若该节点左子树为空,右子树不为空,右子女填补;
若该节点右子树为空,左子树不为空,左子女填补;
若左右子女都不为空,右子树的中序序列的第一个元素填补,其在对该子女进行删除操作
AVL树是以高度之差的绝对值不超过1的二叉搜索树为左右子树的二叉搜索树
树的存储表示
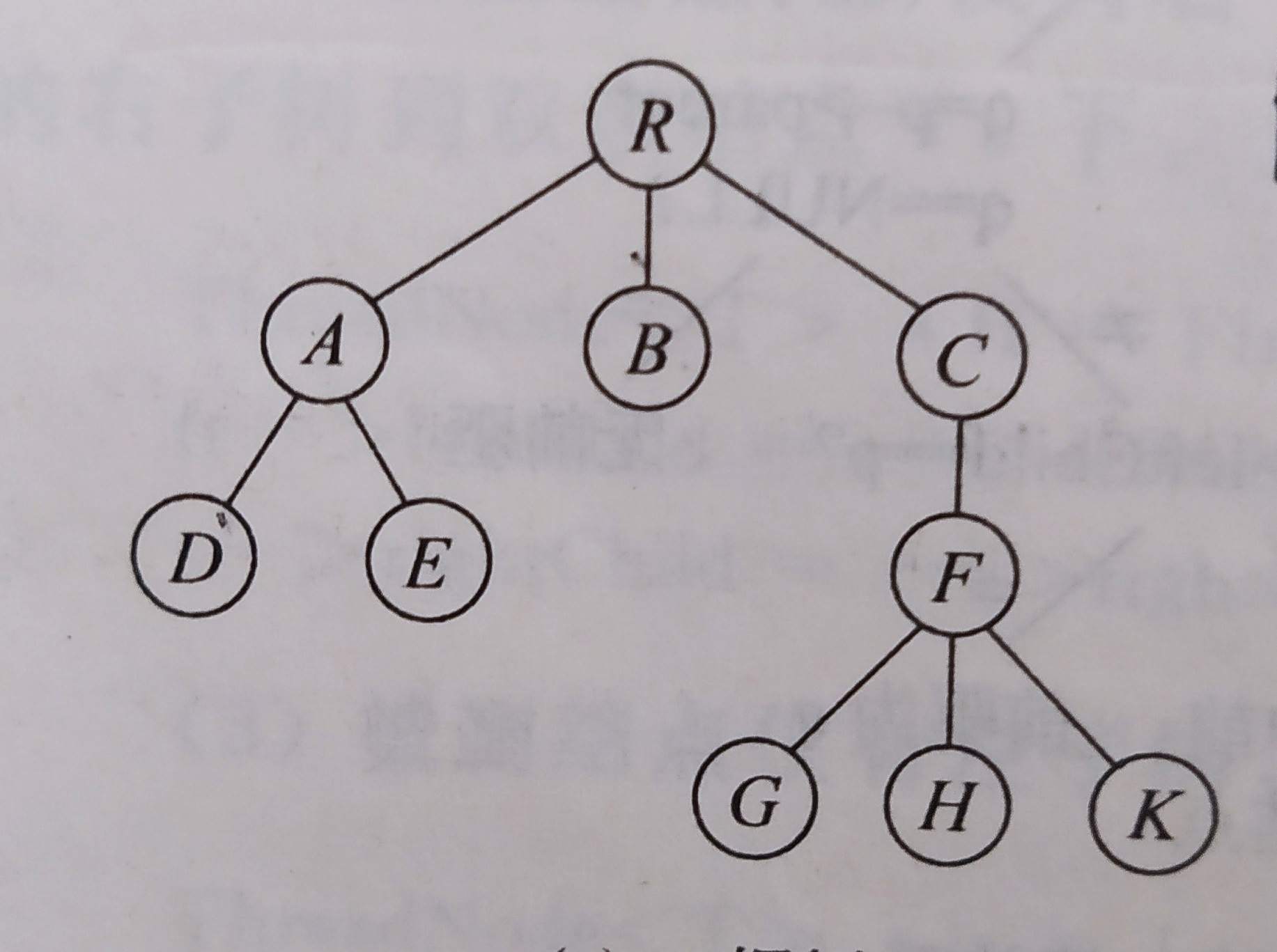
广义表表示法
R(A(D,E),B,C(F))
父指针表示法
子女兄弟链表表示法
子女链表表示法

森林是树的有限集合
森林中的树可以转换为二叉树表示,二叉树表示的根节点都没有右孩子,把每个二叉树表示的根节点连接到上一个根节点的右孩子上,就形成了二叉树表示
森林的深度优先遍历:从左到右对每颗树进行深度优先遍历(包含先根遍历和后根遍历)
森林的广度优先遍历:对所有子树逐层从左到右遍历(即不要求一棵树一棵树地解决,而是所有树一起按顺序解决)
并查集用树表示,,所有集合的全集构成一个森林,支持union操作和find操作
B树又名平衡m路查找树,服从以下规则
1)所有节点至多有m个子树,m-1个关键字
2)对于非终端节点的根节点,至少有1个关键字,2个子树
3)对于根节点外的非终端节点,至少有ceil(m/2)个子树,ceil(m/2)-1个关键字
4)所有节点中,关键字从小到大排列
注意:其叶子节点除了包含关键字之外,也包含指向失败节点的指针;非叶子节点包含关键字或指向关键字的指针
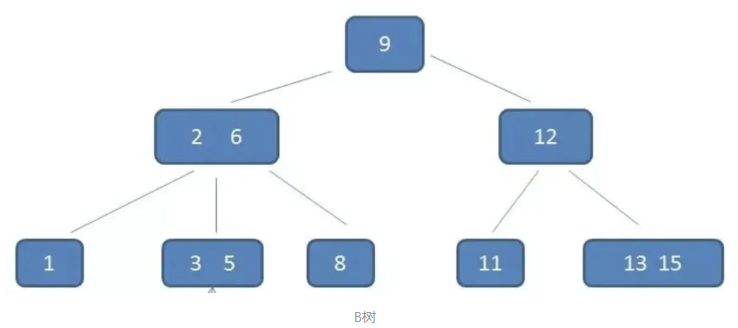
B树的高度范围
假设某个B树有n个关键字,则
对于有n个关键字的B树,失败节点在h+1层,有n+1个,而h+1层至少有 个节点,则
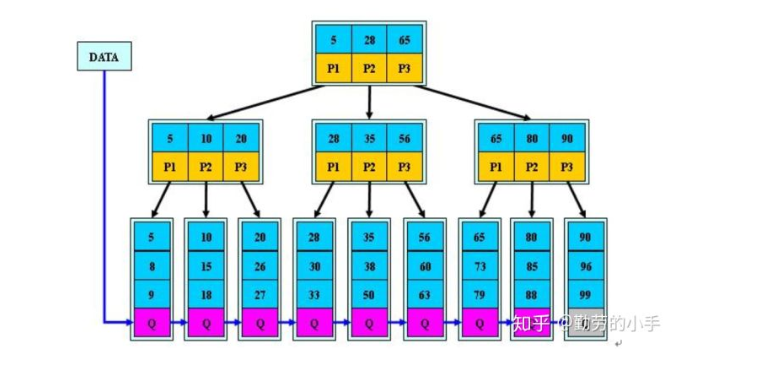
B+树的定义
1)每个节点最多有M棵子树(子节点)
2)根节点最少有1棵子树,除根节点之外,其他节点至少有ceil(/2)棵子树
3)所有叶子节点在同一层,按照从小到大的顺序存放所有关键码,个额叶子节点顺序连接
4)有n个子树的叶子节点有n个关键码(或者n-1个关键码,但是要统一)
5)所有非叶子节点可以看成是叶子节点的索引,每个关键字和指向子树的指针构成索引项