包括:
1)二叉树的先序遍历、中序遍历、后序遍历、层序遍历
2)二叉树的先序和中序序列求得后序序列、二叉树的中序和后序序列求得先序序列
3)线索二叉树:给定根节点,其中序序列的第一个和最后一个节点;给定节点p,求节点p的前驱节点和后继节点
4)堆的构造、堆的插入、堆的删除
5)AVL树的平衡化旋转:左旋转,右旋转,先左后右旋转,先右后左旋转
6)并查集的union操作和find操作
7)B树的插入和删除
1)二叉树的先序遍历、中序遍历、后序遍历、层序遍历
先序遍历
void pre_odr(node* root){
if(root==NULL) return;
printf("%d ",root->val);
pre_odr(root->left);
pre_odr(root->right);
}
中序遍历
void in_odr(node* root){
if(root==NULL) return;
in_odr(root->left);
printf("%d ",root->val);
in_odr(root->right);
}
后序遍历
void post_odr(node* root){
if(root==NULL) return;
post_odr(root->left);
post_odr(root->right);
printf("%d ",root->val);
}
层序遍历
void level_odr(node* root){
queue<node* > que;
que.push(root);
while(!que.empty()){
printf("%d ",que.top()->val);
if(que.top()->left!=NULL)que.push(que.top()->left);
if(que.top()->right!=NULL)que.push(que.top()->right);
que.pop();
}
}
2)二叉树的先序和中序序列求得后序序列、二叉树的中序和后序序列求得先序序列
二叉树的先序和中序序列求得后序序列
void get_post_odr(vector<int>& pre_odr,vector<int>& in_odr,vector<int>& post_odr,int pl,int pr,int il,int ir){
int j;
for(j=il,j<=ir;++j){
if(in_odr[j]==pre_odr[pl]){
break;
}
}
if(j-1>=il)get_post_odr(pre_odr,in_odr,post_odr,pl+1,pl+j-il,il,j-1);
if(j+1<=ir)get_post_odr(pre_odr,in_odr,post_odr,pr+j+1-ir,pr,j+1,ir);
post_odr.push_back(in_odr[j]);
}
二叉树的中序和后序序列求得先序序列
void get_pre_odr(vector<int>& pre_odr,vector<int>& in_odr,vector<int>& post_odr,int pl,int pr,int il,int ir){
int j;
for(j=il,j<=ir;++j){
if(in_odr[j]==post_odr[pr]){
break;
}
}
if(j-1>=il)get_pre_odr(pre_odr,in_odr,post_odr,pl,pl+j-il-1,il,j-1);
if(j+1<=ir)get_pre_odr(pre_odr,in_odr,post_odr,pr+j-ir,pr-1,j+1,ir);
pre_odr.push_back(in_odr[j]);
}
3)线索二叉树:给定根节点,其中序序列的第一个和最后一个节点;给定节点p,求节点p的前驱节点和后继节点
给定根节点,其中序序列的第一个和最后一个节点
node* first_node(node* root){
while(l_tag==0&&root->left!=NULL)root=root->left;
return root
}
node* last_node(node* root){
while(r_tag==0&&root->right!=NULL)root=root->right;
return root;
}
给定节点p,求节点p的前驱节点和后继节点
node* prev_node(node* p){
if(p->l_tag==1)return p->left;
else return last_node(p->right);
}
node* next_node(node* p){
if(p->r_tag==1)return p->right;
else return first_node(p->right);
}
4)堆的构造、堆的插入、堆的删除(以小顶堆为例)
堆的构造
void sift_down(vector<int>& vec,int start,int m){
int i=start,j=2*i+1;
int temp=vec[i];
while(j<=m){
if(j<m&&vec[j]<vec[j+1])++j;
if(temp<=vec[j])break;
else{
vec[i]=vec[j];
i=j;
j=2*i+1;
}
}
heap[i]=temp;
}
void init_heap(vector<int>& vec){
int cursize=vec.size(),curpos=cursize/2-1;
while(curpos>=0){
sift_down(vec,curpos--,cursize-1);
}
}
堆的插入
void sift_up(vector<int>& vec,int start){
int j=start,i=(j-1)/2,temp=vec[j];
while(j>0){
if(vec[i]<temp)break;
else{
vec[j]=vec[i];
j=i;
i=(j-1)/2;
}
}
vec[j]=temp;
}
void ist(vector<int>& vec,int val){
vec.push_back(val);
sift_up(vec,vec.size()-1);
}
堆的删除
bool pop_val(vector<int>& vec,int& val){
if(vec.empty())return false;
val=vec[0];
vec[0]=vec.back();
vec.erase(vec.size()-1);
sift_down(vec,0,vec.size()-1);
}
5)AVL树的平衡化旋转:左旋转,右旋转,先左后右旋转,先右后左旋转
struct node {
int v, h;
node* l, * r;
node() {}
node(int vv, int hh) :v(vv), h(hh) { l = r = NULL; }
};
int geth(node*& r) {
if (r == NULL)return 0;
else
return r->h;
}
void LL(node*& r) {
node* t = r->l;
r->l = t->r;
t->r = r;
r->h = max(geth(r->l), geth(r->r)) + 1;
t->h = max(geth(t->l), geth(t->r)) + 1;
r = t;
}
void RR(node*& r) {
node* t = r->r;
r->r = t->l;
t->l = r;
r->h = max(geth(r->l), geth(r->r)) + 1;
t->h = max(geth(t->l), geth(t->r)) + 1;
r = t;
}
void LR(node*& r) {
RR(r->l);
LL(r);
}
void RL(node*& r) {
LL(r->r);
RR(r);
}
void ist(node*& root, int d) {
if (root == NULL)
root = new node(d, 1);
else if (d < root->v) {
ist(root->l, d);
if (geth(root->l) - geth(root->r) == 2)
if (d < root->l->v)
LL(root);
else
LR(root);
}
else {
ist(root->r, d);
if (geth(root->r) - geth(root->l) == 2)
if (d < root->r->v)
RL(root);
else
RR(root);
}
root->h = max(geth(root->l), geth(root->r)) + 1;
}
6)并查集的union操作和find操作
int findr(vector<int>& root,int a){
//路径压缩
while(a!=root[a]){
tmp=root[a];
root[a]=root[tmp];
a=tmp;
}
return root[a];
}
void uni(vector<int>& root,int a,int b){
int root_a=findr(a);
int root_b=findr(b);
root[root_b]=root_a;
}
7)B树的插入和删除
B树的插入
B树是从空树起,逐个插入关键码而生成。
若插入某节点之后,此节点关键字达到了M个,则对该节点进行分裂操作:
取第ceil(m/2)个元素插入到该节点的父节点中,第1到ceil(M/2)-1个关键字分裂成一个新的节点,第ceil(m/2)+1)到第M个关键字分裂成另一个新节点
B树的删除
当所删除的关键字k在非叶节点中时,有如下三种情况:
1)若小于k的子树的关键字个数>ceil(m/2)-1,则将k替换为k的前驱k',并递归删除k'
2)若大于k的子树的关键字个数>ceil(m/2)-1,则将k替换为k的后继k',并递归删除k'
3)若前后两个子树的关键字个数均为ceil(m/2)-1,则直接将两个子节点合并,如合并后仍需处理子节点的子树,则按照此算法递归处理
当所删除的关键字k在叶子节点中时,有如下三种情况:
1)该节点的关键字个数>ceil(m/2)-1,则删除后仍满足B树定义,所以直接删除
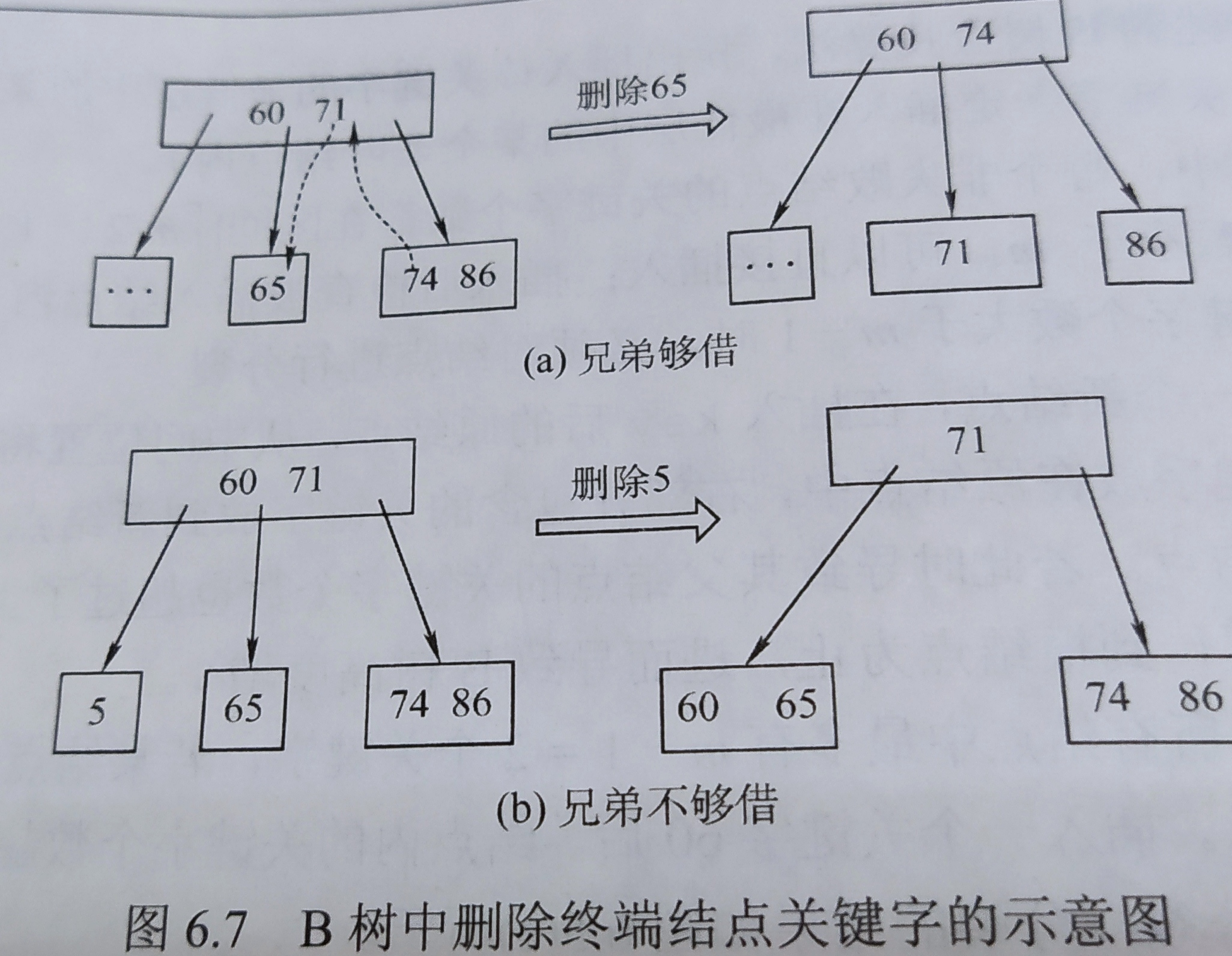
2)删除后该节点的关键字个数<ceil(m/2)-1,若左或右兄弟节点的关键字个数大于ceil(m/2)-1,则将父母节点中左或右关键字下移到该节点,将左或右兄弟节点的最大或最小的关键字上移到父母节点
3)若兄弟节点也不够借,则合并双亲节点中的关键字和兄弟节点