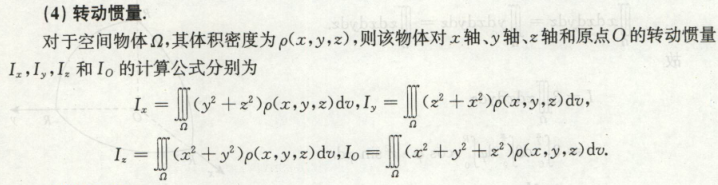设 在平面 上的闭区域 上连续,变换 将平面 上的闭区域 映为平面 上的闭区域 ,且满足
1) 在 上具有一阶连续偏导数
2)在 上,雅可比式
3)变换 是一对一的
则有积分换元公式
普通对称性
即被积函数关于 轴或者 轴对称,此时有 或
轮换对称性
即积分区域关于直线 对称,此时有
极坐标系和直角坐标系的互化
做变量替换 ,则 ,
设 在 上的闭区域 上连续,变换 将 上的闭区域 映为 上的闭区域 ,且满足
1) 在 上具有一阶连续偏导数
2)在 上,雅可比式
3)变换 是一对一的
则有积分换元公式
普通对称性
即被积函数关于平面xOy或平面yOz或平面zOx对称
轮换对称性
即积分区域是以直线 为轴的旋转体,此时有
直角坐标系内的计算
先计算截面上的积分后沿着截面法线积分,或者先沿着法线积分后计算截面上的积分
柱面坐标系
先计算截面后沿着z轴积分
球面坐标系
适用场合:被积函数中含有 或积分区域为球或球的部分亦即锥或锥的部分
变量替换: ,
技巧:
1)对称性应用:使用普通对称和轮换对称适当1)化简直角坐标系的下的积分,再变量替换到球坐标系求解
2)逆用形心公式:
重心
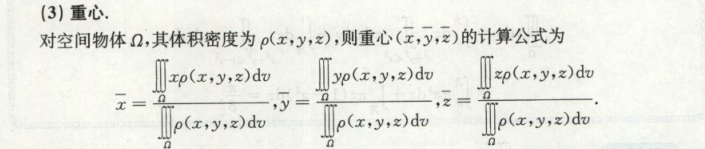
转动惯量