可分离变量的常微分方程以及一阶线性微分方程的解法
解齐次方程、伯努利方程和全微分方程,会用简单的变量代换解某些微分方程
可分离变量方程
可写成 的一阶微分方程称作可分离变量的常微分方程
解法
对 两端进行不定积分 ,解得 称为原方程组的隐式(通)解
两种定义
定义一:若一阶微分方程可以化成 的形式,那么就称此方程为齐次方程
定义二:如果微分方程 中的函数 中的 的次数是一样的(例如m次),即 ,则 微分方程 为齐次方程
解法
做变量替换 ,则 或
化为变量分离方程求解
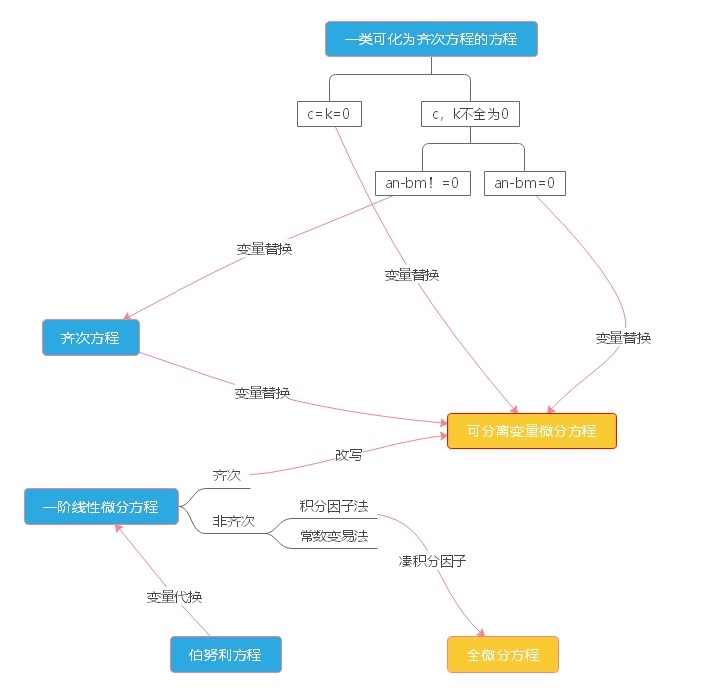
一类可变换为齐次方程的方程及变换方法
讨论形如 的方程
1)当 时,原方程变为 是齐次方程,可化为变量分离方程求解
2)当 不全为0,且 ,方程 有唯一解,解得 ,对 做变换 ,于是原方程变为 是齐次方程,可化为变量分离方程求解
3)当 不全为0,且 ,此时存在 , ,于是原方程变为 ,再做变量替换 ,得到方程 可化为变量分离方程
一阶线性方程
形如 的方程称为一阶线性方程
齐次线性方程与非齐次线性方程
若一阶线性方程的自由项 则称为齐次线性方程,否则称为非齐次线性方程
齐次线性方程的解法——分离变量法
齐次线性微分方程可写作 ,等号两端同时进行不定积分,解得
非齐次线性方程的解法——积分因子法与常数变易法
积分因子法
将方程改写成 ,以因子 乘等号两端,得到一个全微分形式的方程 ,对等号两端进行不定积分,得到 ,于是有通解
常数变易法
假设原方程的解有这样的形式 ,其中 是未知函数,则将 代入原方程 ,得到 ,亦即 ,对等号两端进行不定积分,得 ,则通解为
全微分方程(恰当方程)的定义
考虑一阶微分方程 ,若存在可微函数 ,亦即 ,则称方程 为恰当方程或全微分方程
解的形式
方程为恰当方程的充要条件
方程 为恰当方程的充要条件是
伯努利方程
形如 的方程叫伯努利方程
解法
用变量代换方法将其化为线性方程求解